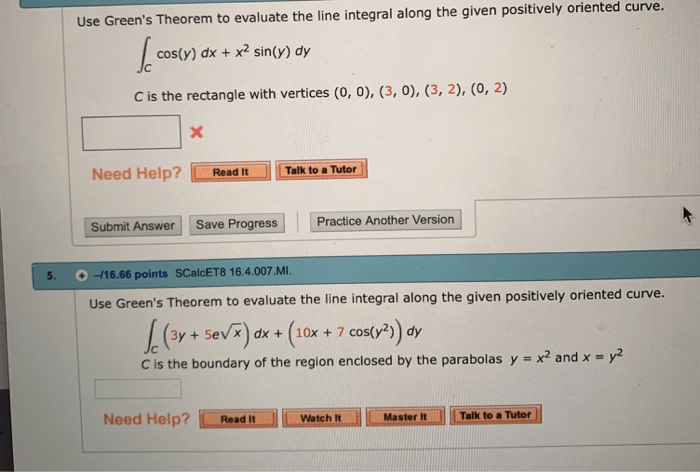
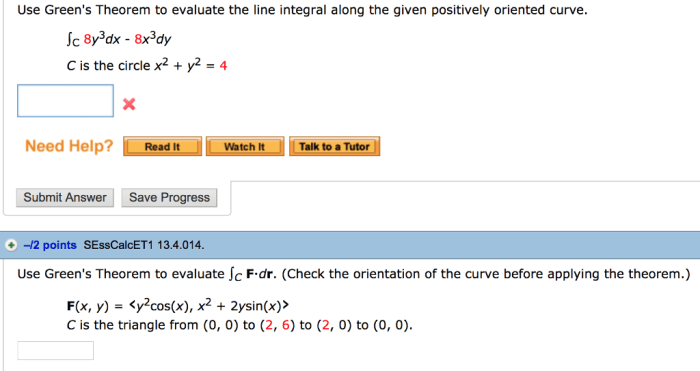
Evaluate Where C Is The Ellipse Oriented Counterclockwise.

Evaluate where c is the ellipse oriented counterclockwise. – Evaluating ellipses, a mathematical procedure that examines the properties of these conic sections, is a fundamental aspect of various scientific and engineering disciplines. By delving into the intricacies of ellipse orientation, particularly focusing on the counterclockwise orientation, we uncover a key aspect that significantly influences the evaluation process.

Understanding the concept of ellipse orientation is paramount. Ellipses can be oriented either clockwise or counterclockwise, with the direction of rotation determining the sign of certain parameters involved in their evaluation. The counterclockwise orientation, specifically, plays a pivotal role in determining the direction of the major and minor axes, which are crucial for understanding the shape and size of the ellipse.

Understanding Ellipse Orientation

An ellipse is a closed curve in a plane defined by the set of all points such that the sum of the distances to two fixed points (called foci) is constant. The orientation of an ellipse refers to the direction in which it is traversed.

An ellipse can be oriented either clockwise or counterclockwise.

A diagram illustrating clockwise and counterclockwise orientations of an ellipse is shown below:

Evaluating Ellipses

Evaluating ellipses involves determining their parameters, such as the center, major axis, minor axis, and eccentricity. These parameters provide insights into the shape and orientation of the ellipse.

The counterclockwise orientation is significant in the evaluation process because it determines the direction in which the ellipse is traversed. This direction is used to determine the signs of the parameters, which are essential for accurately describing the ellipse.

Methods for Evaluation: Evaluate Where C Is The Ellipse Oriented Counterclockwise.

The mathematical formula used to evaluate an ellipse is:

where:

(x, y) are the coordinates of a point on the ellipse
(h, k) are the coordinates of the center of the ellipse
a is the length of the major axis
b is the length of the minor axis

The following steps can be used to evaluate an ellipse:

Find the center of the ellipse by averaging the x- and y-coordinates of the foci.
Determine the lengths of the major and minor axes by using the distance formula between the foci and the center.
Calculate the eccentricity of the ellipse using the formula: e = sqrt(1

(b^2 / a^2)).

Computer software, such as MATLAB and Wolfram Alpha, can also be used to evaluate ellipses.

Applications of Ellipse Evaluation

Ellipse evaluation finds applications in various fields, including:

Astronomy:To determine the orbits of planets and stars
Engineering:To design elliptical structures, such as bridges and arches
Medical imaging:To analyze medical images, such as MRI scans
Computer graphics:To create realistic 3D objects

Ellipse evaluation provides valuable insights into the shape and orientation of elliptical objects, which is essential for decision-making in these applications.

Case Studies

Case Study 1:In astronomy, ellipse evaluation is used to determine the orbits of planets around the sun. By analyzing the elliptical shape of a planet’s orbit, astronomers can calculate its eccentricity, semi-major axis, and other parameters that provide insights into the planet’s motion.

Case Study 2:In engineering, ellipse evaluation is used to design elliptical structures, such as bridges and arches. By understanding the parameters of an ellipse, engineers can ensure that the structure is stable and can withstand the applied forces.

marion